Author: Bastien Milani
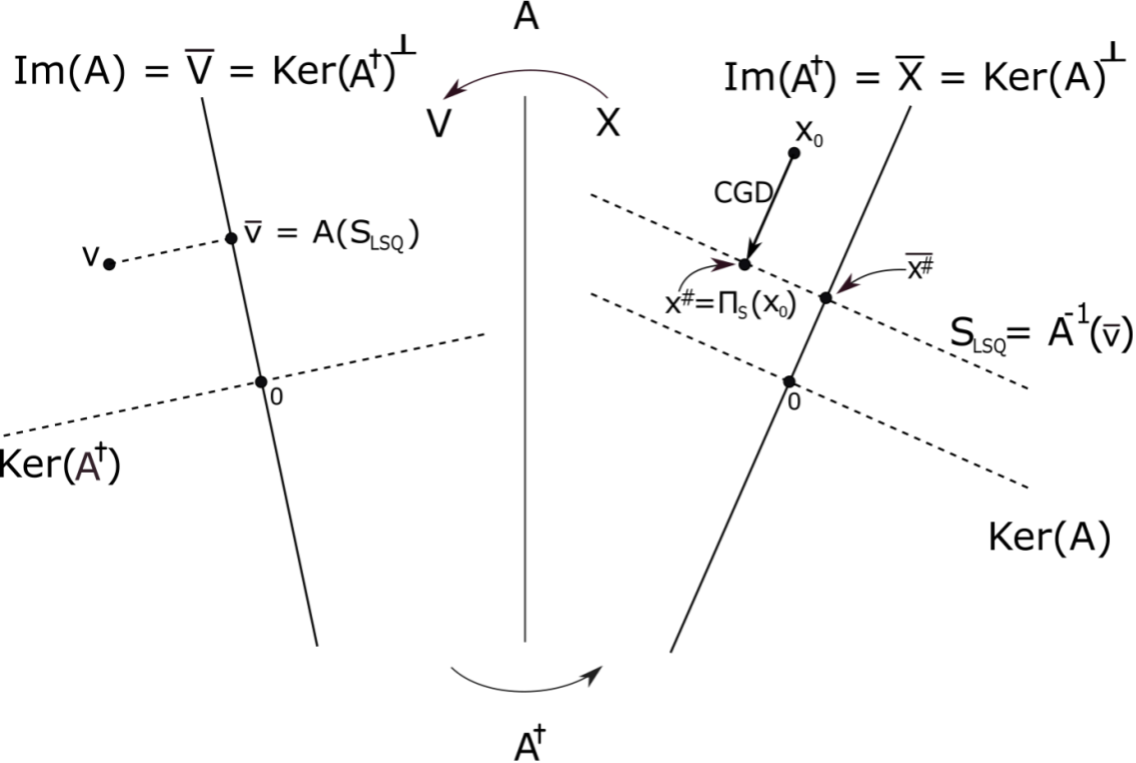
This text describes in detail how to solve a generalized LASSO problem with the ADMM algorithm in the framework of complex Euclidean spaces with non-standard real-valued Euclidean products, which is the framework needed in non-Cartesian MRI reconstruction. In particular, it is explained how to solve the two-terms least-square sub-problem of ADMM with the conjugate gradient descent (CGD) when the Euclidean products are real-valued non-standard and the decision variable is complex valued. We insist in particular on the definition of the adjoint of the problem matrix, which is different from the conjugate transpose in the case of non-standard Euclidean products. One major result presented in this text, which is happily ignored in most of the literature about CGD, is that CGD solves a least-square problem even if the problem matrix is not invertible: in that case is the solution set and affine space and CGD performs the orthogonal projection of the start value on that solution set. A demonstration is provided.


